A Suggested Model for Dark Energy

Edit, 8-17-23: A condensed restatement of my speculation on dark energy as a natural prediction of treating gravity as a nonlocal gauge theory:

A long time ago (2008) I got really curious about dark energy. A common intuition pump is to treat matter’s gravitational effect on spacetime as compression: e.g. spacetime is like a trampoline and big chunks of matter are like balls compressing the trampoline and creating a gradient. Gravity can be thought of as the natural movement of matter down this gradient. But we see a “dark energy” factor which is making the universe expand, and we don’t know where it’s from. What if we extended the trampoline metaphor and treat spacetime as a membrane over something like an incompressible liquid? Local compression somewhere means it will ‘bulge out’ elsewhere. Similar to if you poke your fingers into a water balloon — you push in somewhere, everywhere else bulges a little. Maybe “dark energy” is this nonlocal bulge.

In a perfectly homogenous universe, this would mean the force of gravity would be zero — it would not exist as a force, since it would everywhere be opposed by an exactly equal force. Like trying to squeeze a water balloon evenly everywhere at once — you end up with no change. However, as we shift away from a homogenous state and structure formation occurs, it would be like many small fingers are pushing into spacetime, leading to more bulging elsewhere. Gravity and dark energy would cease canceling each other out.

The core prediction: if this is true we should expect the amount of dark energy to exactly track structure formation: an immediate enormous jump as quantum effects clump matter up, a later jump from nucleosynthesis & EM-driven clumping, and a gradual acceleration during multi-scale star/galaxy/cluster/supercluster formation. If such structure formation ever stopped, dark energy should cease increasing. The timeline (and ultimate trajectory) of dark energy is afaik an open mystery, and this would offer some tightly constrained predictions which are consistent with the (coarse) data we have.

Basically I want to say we could think of gravity as a nonlocal gauge theory, and a result of spontaneous symmetry breaking, but via the gauge theory relationship some underlying symmetry is preserved. Dark energy would be a manifestation of what is preserved under the gauge theory.

I’m not precisely clear whether the relevant magnitudes work out, or how to mathematically characterize total gravitational inhomogeneity, or what scales of structure formation might dominate this inhomogeneity metric. And perhaps the idea of a “global gauge theory” is impossible to formalize in physics-standard terms and we’d need the fields already explored in gravitational gauge theory circles — and at that point maybe this idea is old hat. But it’s fun to speculate on “what happens if we add a conservation law to spacetime compression?” — and from the perspectives of “what aesthetics in physics have proven generative”; “how do other forces work?”; and “Occam’s razor: is it simpler to assume the presence or absence of this conservation law?” I think this is a defensible move.

Edit, 3-10-13: The big bang happened. The universe expanded a lot. Everything was pretty evenly distributed. The universe was a uniform mist of plasma, light, and hydrogen, as far as the eye could see.

After 13.77 billion years, things are no longer so evenly distributed. Matter has clumped up into gas clouds, planets, stars, solar systems, galaxies, clusters, superclusters. Quantum fluctuations during the big bang made things a little uneven, and gravity did the rest.

I’ve been trying to figure out how to quantify just how clumped up matter has become. How to put a number on how gravitationally inhomogeneous the universe is. If a universe with a perfectly even mist of atoms and photons is a 1, what are we?

I have this crazy-and-probably-wrong idea that this quantity, and the amount of dark energy observed throughout cosmological history, might share some eerily similar inflection points. Moreover, these two quantities might be causally connected- e.g., an increase in gravitational inhomogeneity may cause an increase in dark energy.

But I don’t think there’s a good holistic calculation of gravitational inhomogeneity yet. And I am not a very good cosmologist.

The following is an attempt to fumble around for an analogy of why this could be the case. However, I ask theorists to focus less on the analogy and more on the simple, empirical prediction that gravitational inhomogeneity and dark energy will correlate better and better as our measurements of them improve.

Dark Energy, or the unknown force causing the accelerated expansion of the universe, is one of the prime mysteries of modern physics. The following guess as to its nature, as any new theory, is probably wrong– but it’s also elegant, consistent with the provisional data, and falsifiable. I believe it’s worth looking into.

The basic idea is to model spacetime as imperfectly compressible (contrary to the standard implicit assumption of perfect compressibility) and identify Dark Energy as the resulting and proportional ‘pushback’ connected with gravity’s compression of spacetime.

To approach this explanation via analogy– if we take spacetime to be like the surface of a balloon upon which we live, the gravitational compression from aggregated clumps of matter (stars, galaxies, black holes, etc) are like fingers pushing into the balloon. The balloon is imperfectly compressible, thus it’s natural for the balloon to bulge where it’s not being compressed. Furthermore, though its volume stays ~constant[1] as we squeeze it, the balloon (like the universe) appears to expand to any flatlanders: its total surface area increases in relation to how unevenly compression is applied.

Timeline and predictions:

The timeline of massive expansions due to Dark Energy seems to correlate with what we can guess about major thresholds in the de-homogenization of matter. We would expect a massive initial de-homogenization (and thus a massive jump in Dark Energy) right after the Big Bang due to quantum effects, then another during Big Bang nucleosynthesis, another when large-scale matter structures are able to form, and another as matter organizes into very large scale structures such as galaxies, clusters, and superclusters. Eventually, when potential gravitational entropy is exhausted, Dark Energy will cease increasing. As we improve both our models of matter aggregation, and our empirical measurements of the changing contribution of Dark Energy, I predict these timelines — the extent to which matter is clumped up, and the amount of Dark Energy in the universe — will correlate increasingly well.

Dehomogenization and Dark Energy:

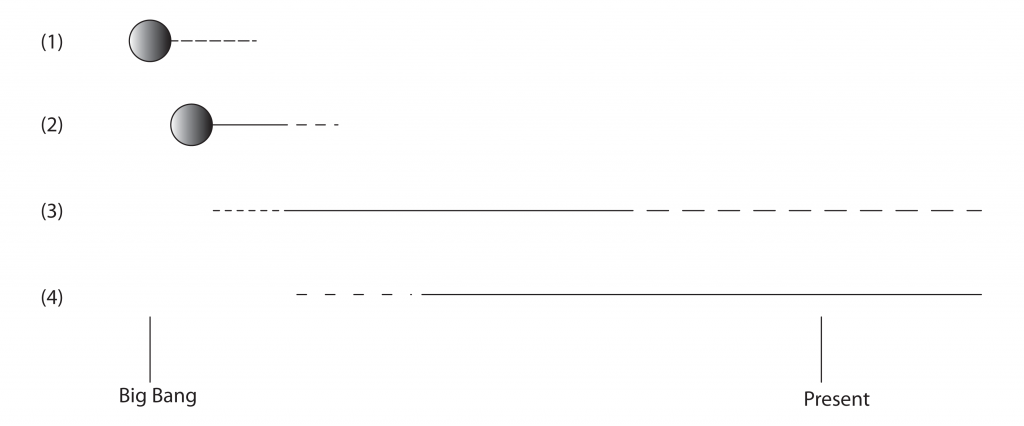
(1): Initial dehomogenization due to quantum effects;

(2): Clumping based on strong/weak/EM interactions (Big Bang nucleosynthesis and EM-based dehomogenization);

(3): Gravitational clumping based on small-scale initial inhomogeneities (planet/star formation);

(4): Gravitational clumping based on larger-scale inhomogeneities (galaxy/cluster/supercluster formation).

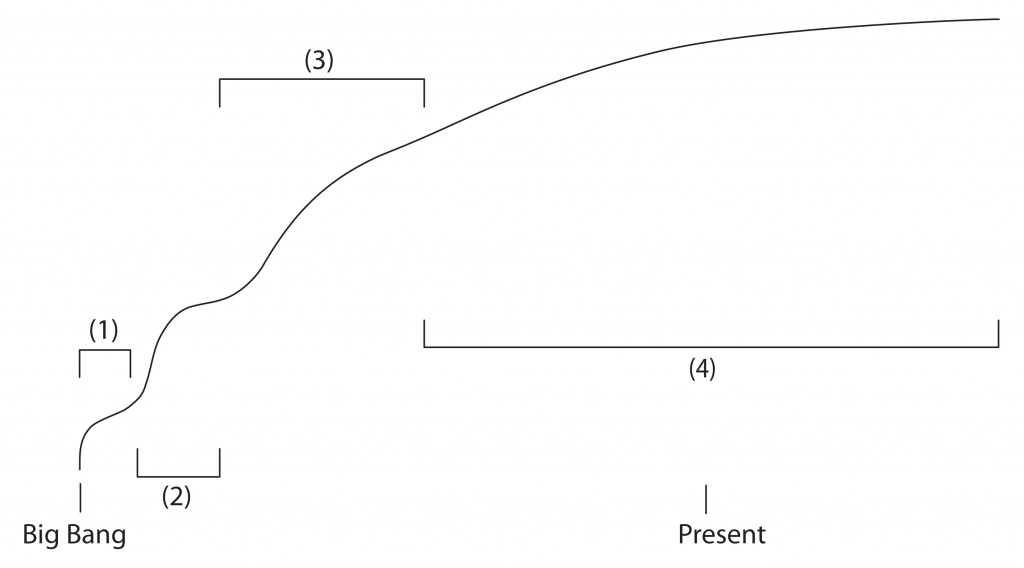
A more precise answer would involve quantifying matter clumping computationally, and deriving exact numbers and timescales. I provide these graphs as an aide to the intuition, and particularly to illustrate inflection points.

Discussion:

– I don’t know the specific mechanism of Dark Energy. Some counterpart carrier particle to the (still theoretical) graviton? A non-localizable property of spacetime? A MOND-like modification of gravity? An emergent property of entropy? I don’t have a reasonable guess.

– This theory seems consistent with the most popular topologies posited for our universe. However, it may be more elegant under certain topologies than others.

– As an explanation-by-correlation-and-analogy, this theory is weak. As a structure which generates definite, falsifiable predictions, this theory is strong. The proof, as they say, will be in the pudding.

Footnotes:

[1] There are really three options here- that spacetime is perfectly compressible, imperfectly compressible, or perfectly incompressible. My theory merely requires that it is not perfectly compressible.

[2] This statement would not be exactly correct, as even a universe with homogeneously distributed matter would have a small dark energy component: only a universe with homogeneously distributed compression would not. But if matter was truly distributed homogeneously this component would presumably be very small and would not be a dehomogenizing force.

[3] How do we quantify how ‘clumped up’ or dehomogenized the matter in the universe is? It’s obviously a problem with a solution, but how to approach the solution isn’t obvious. One option would be to frame this issue in terms of gravitons and how long the average graviton travels before interacting. For instance, and I don’t have a lot of confidence in the following equation, but the type of formulation that might make sense might be something like this:

Within any specific range of times, the amount of Dark Energy should be equal to: Gr(a)*S(a) – Gr(h)*S(h), where

Gr(a) is the actual number of gravitational carrier particles (gravitons?) exchanged in the universe;

Gr(h) is the hypothetical number of gravitons which would be exchanged in a universe of the current size if matter and energy were distributed homogeneously (necessarily equal to or lesser than Gr(a));

S(a) is the scaling factor of how much the average graviton bends spacetime in the current universe;

S(h) is the scaling factor of how much the average graviton would bend spacetime in a hypothetical universe of the current size but where matter and energy were homogeneously distributed — presumably differing from S(a) due to differences in average graviton longevity.

 

I’ll admit my formalizations are rough. But I think the core approach elegantly arises from one assumption, and most importantly makes very specific, falsifiable predictions.

Additional Visual Aids: