On weak vs strong dual-aspect monism
Sometimes, the solutions to the hardest problems are embarrassingly simple, and all that’s lacking is a few dedicated people actually trying to solve things. I often feel this way about formalizing consciousness.
Thus far, I’ve largely focused on mathematizing pleasure/pain; the flagship output has been the Symmetry Theory of Valence. Another frame that I think could be equally generative is taking dual-aspect monism seriously.
Dual-aspect monism?
Dual-aspect monism (aka ‘neutral monism’) essentially argues the physical and the phenomenal are ultimately different aspects of the same thing, similar to different shadows (mathematical projections) cast by the same object. The Stanford Encyclopedia of Philosophy suggests that this model originated with Ernst Mach, William James, and Bertrand Russell; today it has a small but devoted following. Personally, I think that if consciousness is something to be formalized, as opposed to a ‘God of the Gaps’ frame where it’s a leaky abstraction that will shrink to nothing as we sharpen our vocabulary, then dual-aspect monism seems like the most coherent frame (see: Against Functionalism).

Today, though, I want to make a further distinction: there are two versions of dual-aspect monism available to us, the weak version and the strong version. And I think an enormous amount of progress in consciousness research will happen when we start to take the strong version seriously.
Weak vs Strong monism
Weak dual-aspect monism frames its argument as a philosophical solution to consciousness: under this framework, there’s the physical and the phenomenal, and in some sense they’re the same, and this clarifies issues of ontology and causality in the study of consciousness. The resolution of metaphysical confusion about these issues is seen as the victory.
Strong dual-aspect monism, on the other hand, says we shouldn’t stop there. Namely, if the physical and the phenomenal really are mathematical projections from the same object, they’ll have an identical deep structure, and we can ‘port’ theories from one projection to the other. I offer the strongest form of this as the meta-theorem of monism: every true theorem in physics will have a corresponding true theorem in phenomenology, and vice-versa. Literally speaking— if we go through a textbook on physics and list the theorems, ultimately we’ll be able to find a corresponding truth in phenomenology for every single one. I don’t know of any ‘strong dual-aspect monists’ out there doing this— but there should be.
An analogy: much as two shadows ultimately represent the same object, but might display different features, both aspects of the monism will ultimately derive from the same structure, though each may have a different set of explicitly-represented vs hidden variables. However, as we progress on determining invariants of how the shadows behave under different conditions (alternate lighting angles, different rotations of the object, etc), we’ll ultimately settle on mathematically-equivalent laws for each shadow. Essentially, anything we figure out about one shadow should likewise constrain how the other shadow will behave. And this is far from hypothetical: we already have an extensive, elegant, and highly predictive framework for describing the dynamics of one shadow — physics!
Noether’s theorem
An obvious place to start here is Noether’s theorem: that for every symmetry in the mathematical structure which describes our laws of physics, there will be a conserved (invariant) quantity in our physical reality. Conservation of linear momentum, for instance, corresponds to a symmetry (invariance) in how space behaves; conservation of angular momentum to a symmetry in rotational dynamics. If Noether’s theorem is true in physics, and if the meta-theorem of monism is true, this theorem should also apply to phenomenology and should be a gold-mine of heuristics for discovering the invariants of qualia space (as I suggested in Principia Qualia).
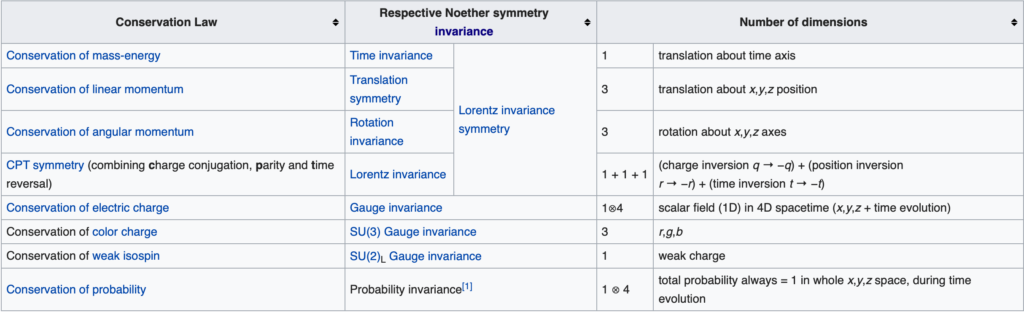
[Added 5-21-22]
Strong monism doesn’t stop at physics
If the Strong monism is true and the domain of phenomenology has an exact parallel in physics, we can keep pulling this thread to explore higher levels of abstraction also. E.g., as physics is to phenomenology, chemistry is to ???. Whole fields are waiting to be discovered here.
Is this a reasonable frame — should we expect to find a phenomenological analogue to Mendeleev’s Periodic Table? It’s worth considering what the periodic table is, where it comes from, and why it’s so useful. My simple model here is that the quantum nature of reality means that some patterns resonate cleanly, and others don’t. (Alternatively put: perhaps the fact that some patterns resonate cleanly, and others don’t, generates the observed quantum structure of reality.) The structures that can persist have strong harmonic structure, e.g. valence shells. This harmonic structure allows clusters of sameness to form, and enforces law-like behavior on combinatorial interactions between different types of clusters, which stays relevant up to the macroscopic scale. We call this mode of analysis “Chemistry” and map its regular structure with the Periodic Table. Ultimately, as homogenous clusters get mixed, the possibility space of stable structures and their interactions undergoes combinatorial explosion, giving way to the complexity of biology and forcing us to use different modes of reasoning.[1]
It would be a really big deal to formalize an analogue for this in phenomenology, because Chemistry explains so much about the building blocks of our world and how these blocks can interact, with so few basic assumptions, and is relevant for almost any scale. The three reasons we might not find something akin to a phenomenological Chemistry seem to be:
- Consciousness is not physical in the way that Strong monism assumes (I believe this is unlikely/incoherent);
- Consciousness is physical and Strong monism is true, but the meta-theorem of monism is only true in a complex way. E.g., although the projections of phenomenology and physics are based on the same fundamental reality as physics, they may support different emergent/secondary structures (such as Chemistry) based on the angle and scale of the projection. This is similar to how one object can cast very different shadows and the structure of one shadow isn’t necessarily a full description of the structure of the other. This will be a matter of degree; all shadows will say something about the structure of other shadows, and insofar as we can change the angle of any shadow, we can explore more common structure. Once we find a few clean results for mapping between the physics and phenomenology ‘shadows’ (such as STV) we dramatically reduce the possibility space for how these shadows could map to each other;
- The meta-theorem of monism is fully true, but only from a God’s Eye view, because of the complexities involved with the binding/boundary problem. I.e., there could be beautiful Chemistry-like structure in phenomenology but we may not be able to recognize it as such, because it’s not consistently bound into a continuous and stateful moment of experience. For instance, perhaps there’s a phenomenological analogue to an endothermic reaction, but the 4d chunk of spacetime it happens across is not a phenomenologically unitary system in the relevant way, so there is no fully experienced phenomenological analogue to this. See e.g. qualia fraggers.
A promising first step for building the phenomenological analogue to Chemistry would be looking for analogues to the basic features of physics which allow Chemistry to emerge. What are the harmonic valence shells of phenomenology? Are there phenomenological analogues to the four fundamental forces, which construct the grammar of phenomenological dynamics and structure at the smallest levels, as they do in physics? What is the hydrogen atom of qualia?
[Added 6-1-23]
Maybe most of the work has been done
It takes two points to define a line; three points for a plane; four for a volume, and so on.
How many points does it take to define a mapping between one projection of reality (physics) and another (consciousness)?
Maybe not many. STV is one point; a solution to the binding/boundary problem would be another.
————
[1] There may be many possible chemical foundations for life (carbon, silicon, etc), but there will tend to be path-dependent lock-in, as biological systems essentially terraform their environments to better support biology. Terran biology can be thought of as a coordination regime that muscled out real or hypothetical competition to become the dominant paradigm on Earth. Perhaps we may find analogues here in past, present, and future phenomenology.
Thank you to Robert Daoust and Adam Barrett for discussion about EM theories of consciousness.